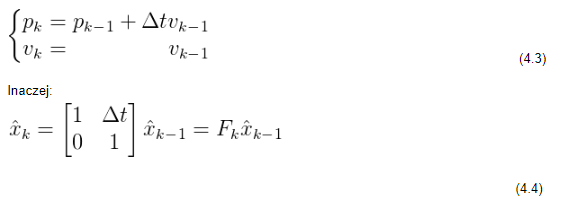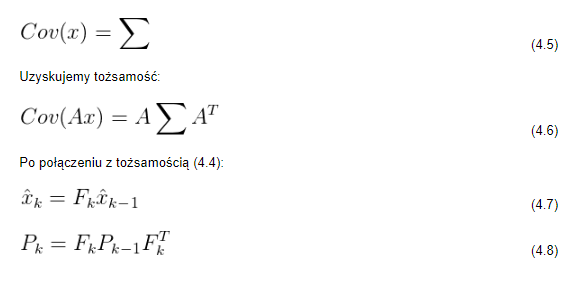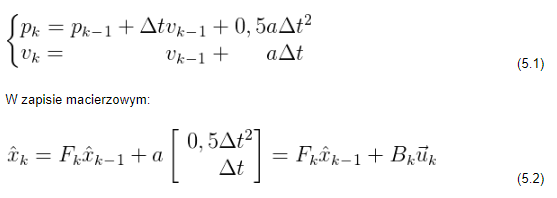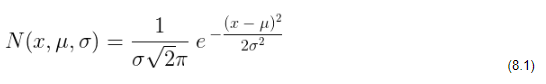Szeroki zakres nauk technicznych potrzebuje odpowiednich narzędzi matematycznych do opisu rozmaitych zjawisk. Zarówno automatyka, robotyka, teoria i układy sterowania, elektronika, elektroakustyka, cyfrowe przetwarzanie sygnałów jak i dziedziny pokrewne opierają się na algebrze liniowej, rachunku operatorowym, algorytmach genetycznych, metodach numerycznych, a także logice rozmytej i innych działach matematyki. Obok popularnych w naukach technicznych narzędzi matematycznych jak transformata Laplace’a, transformata Z, czy metoda elementów skończonych, szczególnie wyróżnia się algorytm, który zrewolucjonizował m.in. kosmonautykę, a jest nim filtr Kalmana. Jest to jedno z klasycznych narzędzi estymacji, które jest używane w takich aplikacjach jak przetwarzanie sygnałów, sterowanie napędami elektrycznymi, układy autonomicznego sterowania pojazdami, a także zarządzanie pracą procesorów w komputerach. W fachowej literaturze filtr Kalmana jest najczęściej opisywany w szczególnych przypadkach aplikacji, takich jak roboty autonomiczne czy liniowe układy regulacji automatycznej z szumem o rozkładzie Gaussa, co znacznie utrudnia przedstawienie zagadnienia od strony fundamentalnej w przejrzysty sposób. Nasz artykuł opisuje dyskretny filtr Kalmana z użyciem rachunku wektorów i macierzy oraz obrazuje praktyczny przykład jego zastosowania.
Czym jest filtr Kalmana?
Filtr Kalmana to specjalny algorytm, który został opracowany i zaprezentowany na początku lat 60. XX w. przez Rudolfa Emila Kalmana (1930-2016) – węgiersko-amerykańskiego inżyniera elektryka. Filtr Kalmana możemy wykorzystać w każdej aplikacji, w której występuje obniżona wiarygodność informacji nt. parametrów układów dynamicznych. Wówczas możemy także przewidywać, jakie zdarzenia mogą wystąpić w następnej kolejności. Dzieje się to na podstawie dotychczas zebranych informacji. Uwzględnia się wówczas wiele czynników warunkowych, które mogą się zmieniać i mieć znaczący wpływ na wynik działania układu automatyki, w którym filtr Kalmana jest zaimplementowany. Ten algorytm znakomicie sprawdza się w układach dynamicznych, w których parametry zmieniają się w sposób ciągły i do prawidłowego funkcjonowania nie potrzebują dużej ilości pamięci, a jedynie stan układu poprzedzający kolejny. Ważnym czynnikiem, który temu sprzyja, jest wysoka szybkość działania algorytmu, dzięki czemu z powodzeniem jest implementowany w aplikacjach czasu rzeczywistego oraz w systemach wbudowanych.
Filtr Kalmana – w jakich aplikacjach warto go zastosować?
Zanim zobrazujemy algorytm przedstawiający zasadę działania filtru Kalmana, posłużymy się jednym ze sprzętowych przykładów jego zastosowania, a będzie nim robot, który może przemieszczać się po gęsto zadrzewionych terenach leśnych. Musi on dokładnie znać swoją lokalizację w celu prawidłowego działania wbudowanego systemu nawigacji.
Możemy wówczas powiedzieć, że nasz robot jest określony za pomocą zmiennej stanu xk, , która to zmienna jest definiowana za pomocą wektora mającego dwie składowe – pozycję p i prędkość v:
(3.1)
Stan układu jest określony przez dane liczbowe określające jego podstawową konfigurację i mogą to być dane liczbowe dla dowolnych wielkości. W naszym przypadku tymi wielkościami są pozycja i prędkość, ale dla innych układów mogą to być także pozostała ilość paliwa w zbiorniku w samochodzie, temperatura grota w kolbie stacji lutowniczej, prąd w obwodzie wzbudzenia generatora synchronicznego i wiele innych parametrów, które w zależności od aplikacji wymagają śledzenia wartości. Robot w prezentowanym przykładzie jest wyposażony w system nawigacji GPS, który jest w stanie określić jego współrzędne z dokładnością do dziesięciu metrów. Jest to wynik zadowalający, ale jest wymagane, aby wbudowany system GPS był jeszcze bardziej dokładny z uwagi na zmienność rozmaitych parametrów terenu, po którym robot się porusza. W najgorszym wypadku przy dokładności pomiaru współrzędnych co do dziesięciu metrów robot może nawet spaść w przepaść.
Przy dokładnym wyznaczeniu toru ruchu robota niezbędna jest znajomość parametrów poszczególnych sygnałów sterujących jego zespołem napędowym – wówczas system GPS ,,wie”, że gdy robot przemieszcza się wykonując ruch quasi-prostoliniowy, to w następnym kroku będzie on prawdopodobnie kontynuował ruch w ten sam sposób i w tym samym kierunku. W dalszym ciągu jednak,robot nie będzie otrzymywał informacji nt. czynników środowiskowych, które mogą wpływać na jego ruch, np. za sprawą podmuchów wiatru, śliskiego podłoża, a także nierówności terenu i przeszkód drogowych uprzednio nieprzewidzianych (np. leżące konary drzew). Wówczas liczba obrotów wykonywanych przez koła jezdne robota, może nieprawidłowo odwzorowywać jego przemieszczanie, wskutek czego wynik przewidywania kolejnego kroku opisującego przemieszczenie robota, może okazać się błędny.
Czujniki systemu GPS dostarczają pośrednich informacji o stanie układu (robota) nt. jego sposobu poruszania się po torze jazdy, ale z ograniczoną dokładnością. Niemniej jednak, okazuje się, że dane otrzymywane z czujników GPS, można użyć w procesie estymacji (szacowania), dzięki czemu możemy uzyskać pomiar współrzędnych o zwiększonej dokładności. Właśnie m.in. w takim celu sprawdza się algorytm znany jako filtr Kalmana.
Filtr Kalmana – początek algorytmu
Aby rozpocząć algorytm filtru Kalmana, zapiszmy równanie wektora stanu (3.1) w postaci macierzowej:
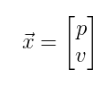
Nie znamy obecnej pozycji i prędkości obiektu, ponieważ istnieje określony zbiór obejmujący cały zakres możliwych kombinacji pozycji i prędkości, które mogą się okazać zgodne z rzeczywistością, ale pośród nich są takie, które są mniej jak i bardziej zgodne z rzeczywistymi wartościami. Algorytm filtru Kalmana zakłada, że obie zmienne stanu (w badanym przypadku są to pozycja i prędkość obiektu) są rozłożone wg rozkładu Gaussa (rozkładu normalnego). Każda ze zmiennych ma swoją wartość średnią, która znajduje się w środkowym położeniu rozkładu losowego i jest jednocześnie wartością oczekiwaną oraz wariancję, która określa niepewność pomiaru. Z pozoru, pozycja i prędkość obiektu nie są ze sobą powiązane, co oznacza, że informacja o stanie pojedynczej zmiennej (składowej wektora stanu) nie będzie wystarczająca do określenia drugiej zmiennej. W rzeczywistości, pozycja i prędkość obiektu są względem siebie powiązane, tzn. prawdopodobieństwo zaobserwowania szczególnej wartości zmiennej określającej pozycję obiektu jest zależne od jego prędkości.
Taka sytuacja może wystąpić przykładowo wtedy, gdy znając poprzednią pozycję obiektu próbujemy ustalić jego aktualną pozycję. Jeśli prędkość obiektu będzie zbyt wysoka, wówczas następny wykonany pomiar pozycji obiektu będzie bardziej odległy. Jeśli natomiast obiekt będzie poruszał się z mniejszą prędkością, wówczas pomiar pozycji w porównaniu do poprzedniego pomiaru będzie wykazywał przemieszczenie obiektu o mniejszą odległość niż przy większej prędkości. Związek między pozycją a prędkością obiektu, jest bardzo ważny przy jego śledzeniu, ponieważ daje cenną informację – pojedynczy pomiar parametrów naprowadza na potencjalne wyniki kolejnych pomiarów tych samych parametrów. Jest to główny cel algorytmu filtru Kalmana – zebranie jak największej ilości danych obarczonych niedokładnością pomiaru w celu uzyskania najbardziej możliwie dokładnego wyniku pomiaru. Relację między zmiennymi stanu określa macierz kowariancji i każdy element wchodzący w jej skład. Wówczas element określa stopień korelacji między i-tą zmienną stanu a j-tą zmienną stanu, przy czym macierz kowariancji jest macierzą kwadratową, tj. liczba jej wierszy jest taka sama jak liczba kolumn.
Zapis macierzowy
W celu modelowania stanu obiektu pomocne jest użycie zapisu macierzowego z wykorzystaniem rozmycia Gaussa – wówczas potrzebujemy dwóch równań dla określenia stanu obiektu dla k-tego pomiaru. xk jest wektorem wartości średnich (skalarnych), które są wartościami oczekiwanymi, a Pk jest macierzą kowariancji.
W niniejszym przypadku rolę zmiennych stanu pełnią pozycja i prędkość obiektu, ale trzeba zaznaczyć, że stan może opisywać dowolna liczba zmiennych reprezentujących dowolne parametry. Następnie należy zwrócić uwagę na wartości zmiennych dla obecnego stanu (w chwili k-1) celem przejścia w proces przewidywania wartości dla stanu w chwili k. Nie jest wiadome, który stan odzwierciedla rzeczywiste parametry obiektu, ale jest to nieistotne dla procesu przewidywania. Etap przewidywania można zobrazować za pomocą wektora Fk. Każdy punkt znajdujący się w przestrzeni stanu w obecnym kroku, zostaje przesunięty w nowy obszar – obszar wartości przewidywanych, w który system się przemieszcza, jeśli poprzedzająca przestrzeń stanu została prawidłowo zlokalizowana. Aby znaleźć przewidywaną przestrzeń stanu znając obecne wartości zmiennych stanu określających pozycję i prędkość, należy skorzystać z układu równań:
W ten sposób uzyskujemy macierz przewidywania, która zawiera informacje o następnym (po k-1) stanie (k). Niemniej jednak, w dalszym ciągu nie wiadomo jak prawidłowo uaktualnić macierz kowariancji. W tym miejscu, każdy punkt zawarty w dystrybucji, trzeba pomnożyć przez macierz A:
Wpływ czynników zewnętrznych
Na obecnym etapie, nie wszystkie czynniki zostały jeszcze uwzględnione, a są to czynniki, które nie są bezpośrednio związane z własnościami układu badanego, lecz występują niezależnie, ale również mogą wpływać na stan układu. Przykładowo, jeśli obiektem opisanym przez zmienne stanu jest elektrowóz (lokomotywa elektryczna) – kiedy maszynista zwiększa napięcie zasilania silników np. przez zmniejszanie strumienia magnetycznego w obwodzie wzbudzenia, lokomotywa przyspiesza. Podobnie, w opisywanym przypadku robota, pokładowy system nawigacji może napotkać na problemy z nadaniem sygnału do układu sterowania robota w celu obrócenia kół lub zatrzymania, np. kiedy zaistnieje niebezpieczeństwo przewrócenia robota pod wpływem wiatru w czasie jazdy. Znając tę dodatkową informację o warunkach zewnętrznych, można ją uwzględnić za pomocą wektora
k, umożliwiając uwzględnienie korekcji w macierzy przewidywania:
Zakładając, że na podstawie sygnałów sterujących (np. współczynnika wypełnienia sygnału sterującego prędkością obrotową silnika), znamy spodziewaną wartość przyspieszenia a, otrzymujemy układ równań:
k jest wektorem sterowania – w prostych układach, w których nie występuje wpływ czynników zewnętrznych, można te składniki pominąć. A co jeśli przewidywane rozwiązanie w dalszym ciągu jest za mało dokładne?
Niepewność zewnętrzna
Cały proces przewidywania trwa bezproblemowo, kiedy stan obiektu bazuje na wszystkich uwzględnionych czynnikach, również tych zewnętrznych, których występowanie nie jest związane z własnościami samego układu, na który one wpływają. Jest tak dopóty, dopóki znamy maksymalne parametry czynników zewnętrznych, na które układ będzie odporny. A co jeśli pojawią się czynniki, o których nie wiemy? Przykładowo, drony (a także inne statki powietrzne) są narażone na podmuchy wiatru, który może zakłócić tor lotu, powodując nawet kolizję z pobliskim obiektem (np. z drzewem). Robot kołowy podczas jazdy, może wpaść w poślizg, wskutek czego mimo obracania się kół, nie będzie mógł ruszyć w dalszą drogę. Wówczas z powodu nieuwzględnienia tych czynników, algorytm na etapie przewidywania może zawieść, co może nieść za sobą nawet nieodwracalne uszkodzenie układu.
Aby zwiększyć prawdopodobieństwo wystąpienia takich wysoce niepożądanych skutków, w obliczeniach należy uwzględnić dodatkową niepewność dla każdego kroku przewidywania. Wówczas w oryginalnym szacowaniu, pierwotna estymacja zostaje rozszerzona o zakres stanów. Rozwiązanie przewidywane xk-1, zostaje przeniesione w obszar kowariancji Qk. Inaczej można także powiedzieć, że czynniki zewnętrzne będące źródłem dodatkowych niepewności, stanowią szum kowariancji Qk. Takie działanie, powoduje powstanie nowego rozmycia Gaussa, które charakteryzuje się inną kowariancją względem pierwotnego rozmycia Gaussa, ale taką samą oczekiwaną wartość zmiennej stanu. Wówczas, otrzymujemy rozszerzoną kowariancję poprzez uwzględnienie czynnika Qk:
Innymi słowy, uaktualniona ,,najlepsza” wartość oczekiwana jest przewidywana na podstawie poprzedniej wartości oczekiwanej z uwzględnieniem wpływu warunków zewnętrznych. Również nowo wyprowadzona niepewność zewnętrzna, jest wynikiem połączenia poprzednio wyliczonej niepewności zewnętrznej z uwzględnieniem rozszerzonej niepewności wynikającej z wpływu warunków zewnętrznych. Na obecnym etapie, możemy poddać dalszej obróbce dane z czujników pomiarowych.
Przybliżanie estymacji na podstawie pomiarów
Badany układ może być wyposażony w kilka czujników pomiarowych, które dostarczają informacji niezbędnych do określenia jego stanu. Niezależnie od tego, na jakie bodźce te czujniki reagują, dostarczają one informacje niezbędne do określenia pozycji i prędkości robota, więc za ich pomocą są wykonywane pomiary pośrednie. Należy zwrócić uwagę na możliwość wystąpienia rozbieżności między jednostkami i skalą odczytu a jednostkami i skalą odczytu śledzonego stanu. W związku z tym, opis czujników jest zamodelowany za pomocą macierzy Hk. Rozmieszczenie odczytów z czujników można przewidzieć na podstawie równań:
Jedną z największych zalet algorytmu filtru Kalmana jest odporność na niedokładność pomiaru dokonywanego przez czujniki (z uwagi na szum). Czujniki mogą być zawodne, wskutek czego każdy oszacowany stan układu może być wynikiem zakresu parametrów odczytywanych przez czujniki. Filtr Kalmana niweluje ten problem do minimum. Na podstawie każdego zaobserwowanego odczytu danych z czujników pomiarowych możemy przypuszczać, że badany układ był w szczegółowo określonym stanie. Jednak z powodu obecności niepewności pomiarowej kilka przewidywanych stanów może być bardziej prawdopodobnych względem innych znajdujących się w zakresie odczytów czujników. W tym celu,wprowadzamy kowariancję niepewności Rk, wynikającą z szumu wprowadzanego przez czujniki oraz wektor średniej wartości odczytu zaobserwowanego k. W ten sposób uzyskujemy dwa obszary rozmycia Gaussa – pierwszy wynikający z przewidywanego odczytu, a drugi z rzeczywistego odczytu z czujników. Dzięki temu obszar poszukiwań optymalnego rozwiązania znacząco zawęża się i cały algorytm można wykonać od nowa w ten sam sposób, uzyskując jeszcze bardziej dokładne, tzn, jeszcze bardziej zgodne z rzeczywistością wyniki obliczeń na podstawie uzyskanych wcześniej danych pomiarowych.
Wzmocnienie Kalmana
Do wyznaczenia macierzy określającej wzmocnienie Kalmana, niezbędne jest wykorzystanie jednowymiarowej krzywej Gaussa uwzględniającej 2 i wartość średnią:
Mnożąc przez siebie równania krzywych obrazujących rozkład normalny dla stanu przewidywanego i stanu rzeczywistego wyznaczonego na podstawie danych odczytanych z czujników pomiarowych uzyskujemy nowe równanie krzywej, której rozkład zawęża zakres wartości dla poszukiwanego wektora stanu:
Stosując zapis macierzowy uzyskujemy:
gdzie K jest macierzą określającą wzmocnienie Kalmana.
Obliczenia końcowe
Otrzymujemy dwie dystrybucje opierające się na rozkładzie Gaussa. Pierwsza z nich jest otrzymana na podstawie pomiaru przewidywanego (9.1), a druga na podstawie pomiaru zaobserwowanego.
Z układu równań (9.3), wyznaczamy warunki określające wspólny obszar dystrybucji (9.1) i (9.2).
W zależności od potrzeb aplikacji, w celu uzyskania jeszcze bardziej dokładnych wyników, cały algorytm można wielokrotnie powtarzać.
Filtr Kalmana – FAQ
Czym jest filtr Kalmana? Filtr Kalmana to algorytm stworzony przez Rudolfa Emila Kalmana węgiersko-amerykańskiego inżyniera, który żył w latach 1930-2016. Najważniejszą cechą filtra jest uniwersalne zastosowanie. Oznacza to, że z powodzeniem można go zastosować we wszystkich aplikacjach, w których zachodzi ryzyko występowania niskiej wiarygodności informacji. Obniżona wiarygodność danych może dotyczyć m.in. parametrów określający układy dynamiczne. Filtr Kalmana wyróżnia się wysoką szybkością działania całego algorytmu, co dodatkowo rozszerza jego zastosowanie.
Filtr kalmana znajduje zastosowanie w różnego rodzaju układach dynamicznych. Szczególnym przypadkiem zastosowania filtru Kalmana są układy działające w oparciu o parametry, które zmieniają się w tak zwany ciągły sposób. Oznacza to, że taki układ nie wymaga dużej ilości pamięci do prawidłowego działania. Wystarczy stan układu, który poprzedza następny układ (jego stan). Filtr Kalmana można z powodzeniem implementować w robotach wyposażonych m.in. w system nawigacji GPS. Kolejne zastosowania obejmują aplikacje czasu rzeczywistego, a także systemy wbudowane.
Jak oceniasz ten wpis blogowy?
Kliknij gwiazdkę, aby go ocenić!
Średnia ocena: 4.4 / 5. Liczba głosów: 13
Jak dotąd brak głosów! Bądź pierwszą osobą, która oceni ten wpis.