Spis treści:
- 1 Algebra Boole’a w programowaniu
- 2 Funktory logiczne
- 3 Układy logiczne
- 4 Nazewnictwo stanów
- 5 Bramki logiczne w układach cyfrowych
- 6 George Boole
- 7 Algebra Boola – zasady
- 8 Rodzaje bramek logicznych
- 9 Bramka NOT
- 10 Bramka AND
- 11 Bramka NAND (-AND)
- 12 Bramka OR
- 13 Bramka NOR
- 14 Bramka XOR (lub inaczej EXOR)
- 15 Prawa logiczne
- 16 Bramki logiczne – FAQ
Bramki logiczne to narzędzia stanowiące elementy konstrukcyjne maszyn, automatów czy robotów. Komputery, z których obecnie korzystamy, wykorzystują miliony mechanizmów logicznych nazywanych bramkami cyfrowymi (lub inaczej bramkami logicznymi). Są to elementy elektroniczne, które przyjmują sygnały binarne na wejściach i zwracają wartości 1 lub 0 – prawda lub fałsz.
Bramki logiczne stanowią stałe elementy konstrukcyjne wielu maszyn. W dzisiejszych czasach najczęściej są to układy scalone, składające się z wielu odpowiednio połączonych tranzystorów. Podobny efekt można uzyskać, korzystając na przykład z urządzeń hydraulicznych lub pneumatycznych. W uproszczeniu zasada działania bramek polega na podaniu jednego z dwóch napięć elektrycznych (poziomów logicznych). Jest to napięcie o wartościach w granicach między 0 V a 0,8 V (poziom 0 – fałsz), natomiast druga wartość napięcia powinna zawierać się w przedziale między 2 V a 5 V (poziom 1 – prawda). Rozróżnienie tego typu – przy pomocy takiej wartości napięć – stosuje się w układach typu TTL (Transistor-Transistor-Logic).

Algebra Boole’a w programowaniu
Algebra Boole’a to rodzaj struktury algebraicznej – jeżeli jesteś programistą i nie znałeś bezpośrednio tego pojęcia, prawdopodobnie szybko domyślisz się, na czym ono polega. Algebra Boola ma szerokie spektrum zastosowań. W wielu językach programowania stosuje się tak zwany typ boolowski (na przykład zmienne boolowskie albo funkcje boolowskie, określane również jako funkcja logiczna) – są to między innymi języki takie, jak Pascal, C++, C#, PHP czy Java. Zmienna boolowska lub wynik funkcji boolowskiej jest w stanie przyjmować tylko jedną z dwóch wartości – 0 lub 1. Typ boolowski stosuje się określania wyniku funkcji (prawda lub fałsz) i oznaczania zdarzeń „flagą”, a także wykorzystuje się jako warunek instrukcji warunkowej lub na przykład jako warunek wyjścia albo kontynuowania pętli.
Funktory logiczne
Zwane są również funktorami zdaniotwórczymi, to wyrażenie, które razem z argumentami funktora, czyli innymi wyrażeniami, stanowi funkcję zdaniową, lub też zdanie.
Algebra Boola – wzory
[zdjęcie ukazujące wszystkie wzory Algebry Boole’a]
Układy logiczne
Nazywa się je również układami cyfrowymi. Operują one na wartościach dyskretnych. Tworzy się je na podstawie bramek logicznych, które realizują podstawowe operacje logiczne, takie jak iloczyn, negację, czy sumę.
Nazewnictwo stanów
Poziomy napięć odpowiadają bezpośrednio wartościom logicznym z algebry Boole’a. Poziom logiczny równy zeru często oznaczany jest literką F (od angielskiego false, czyli “fałsz”) lub L (od angielskiego low – chodzi o “niski” poziom). Analogicznie oznaczany jest poziom równy 1 – często stosuje się oznaczenie literą T (od angielskiego true, czyli “prawda”) lub H (od angielskiego high – chodzi o “wysoki” poziom).

Bramki logiczne w układach cyfrowych
We wnętrzu komputera nieustannie odbywają się operacje, podczas których komputer korzysta właśnie z bramek logicznych – poziomy napięć są odpowiednikiem bitów. Bramka logiczna na swoim wyjściu zwraca odpowiednie napięcie elektryczne, które ponownie mieści się w określonym powyżej przedziale i oznacza jeden z dwóch stanów (1 – prawda lub 0 – fałsz). Wynika ono z funkcji logicznej realizowanej przez bramkę (czyli na przykład koniunkcja, negacja czy alternatywa). Bramki logiczne, które stosowane są w elektronice, to urządzenia wykorzystujące odpowiednio połączone elementy elektroniczne – są to przede wszystkim tranzystory, kondensatory, diody półprzewodnikowe i rezystory (oporniki). Dzisiejsze procesory składają się z miliardów bardzo niewielkich, odpowiednio połączonych tranzystorów. Są one kluczem do działania każdego układu cyfrowego. Każdy tranzystor posiada trzy elektrody – źródło, dren i bramkę. Po przyłożeniu napięcia do ostatniej z nich zmienia się przewodnictwo kanału. Taka znajomość działania tranzystorów jest wystarczająca do dobrego zrozumienia zasady działania bramek logicznych. Bramki logiczne można również postrzegać po prostu jako niewielkie czarne skrzynki, na których wejście podaje się napięcia, aby na wyjściu pojawiło się napięcie wynikowe zależne od funkcji (sygnału wejściowego). Podejście tego rodzaju jest w pełni wystarczające, aby można było zaprojektować nawet najbardziej złożone sieci cyfrowe.
George Boole
Algebra Boole’a to rodzaj struktury algebraicznej, którego nazwa pochodzi od nazwiska znanego filozofa, matematyka i logika George’a Boole’a. Ze względu na wprowadzenie pojęcia algebry Boole’a został uznany za jednego z twórców logiki matematycznej oraz informatyki. Przyszedł on na świat drugiego listopada 1815 roku w Lincoln i dożył roku 1859. Urodził się w rodzinie, w której ojciec był szewcem – ten chciał go posłać do dobrej szkoły, ale z racji braku odpowiednich środków finansowych nie mógł tego zrobić. Nauczył syna wszystkiego, co potrafił i nakłonił do nauki łaciny, która stanowiła wtedy rodzaj przepustki do wyższych sfer. George uczył się z książek, a jako nastolatek zaczął nauczać w szkołach elementarnych. Kiedy skończył około 20 lat, zapoznał się z dziełami Josepha Lagrange’a i Pierre’a Laplace’a i zaczął pisać własne prace na temat matematyki. Pierwsze z nich były źle zredagowane, ale niestety George nie miał środków finansowych, aby poprawić swój warsztat na uczelni.
Mimo wszystko jego prace stały się na tyle znane i były tak ważne, że w 1844 roku otrzymał medal Royal Society. Później – mimo braku oficjalnego wykształcenia – został przyjęty na uczelnię na stanowisko profesora. W 1854 roku opublikował swoją najważniejszą pracę o tytule “An Investigation of the Laws of Thought, on which are founded the Mathematical Theories of Logic and Probabilities” (z angielskiego: “Badanie praw myślenia, na których oparte są matematyczne teorie logiki i prawdopodobieństwa”). Przyczynił się bezpośrednio do stanu, w jakim dzisiaj znajduje się technika cyfrowa – działanie milionów komputerów i urządzeń na świecie działa dzięki wykorzystaniu w nich zasad algebry Boole’a.

Algebra Boola – zasady
Algebra Boole’a definiuje następujące podstawowe prawa:
I – Prawo przemienności dodawania i mnożenia. Oznacza, że wynik wyrażenia a x b jest równoważny do wyniku wyrażenia b x a (przy czym znak “x” oznacza znak mnożenia). Znak równości można postawić między wyrażeniem a + b oraz b + a.
II – Prawo łączności mnożenia. Oznacza, że wynik działania a x b x c jest taki sam jak wynik a(b x c) oraz (a x b)c. Taka sama zasada odnosi się do dodawania – prawo łączności dodawania – wynik wyrażenia a+b+c jest równy wynikowi (a+b)+c oraz a+(b+c)
III – Prawo rozdzielności mnożenia względem dodawania. Wyrażenie a(b+c) jest równoznaczne z wyrażeniem (a × b)+(a × c). Rozdzielność zachodzi również z lewej strony, ponieważ mnożenie jest przemienne: (b+c) x a = b x a + c x a.
Rodzaje bramek logicznych
Działanie bramek logicznych można łatwo rozpisać za pomocą tak zwanych tablic prawdy. Opisuje się w nich kolejne kombinacji stanów wejściowych oraz odpowiadające im stany na wyjściu bramki.
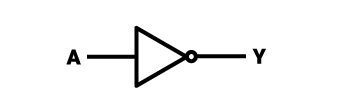
Bramka NOT
Bramka NOT pod względem działania jest najprostsza ze wszystkich tu opisanych (i ogólnie wśród wszystkich wykorzystywanych bramek logicznych). Jej działanie polega na negacji (odwróceniu) sygnału, który otrzyma na wejściu. W praktyce wygląda to następująco: jeżeli na wejściu zostanie nadany sygnał o wartości 1 (prawda), to na wyjściu pojawi się sygnał o wartości 0 (fałsz). Natomiast jeżeli na wejściu pojawi się sygnał 0, na wyjściu pojawi się 1.
Przykład 1:
wejście = 1
wyjście = 0
Przykład 2
wejście = 0
wyjście = 1
Bramkę NOT przedstawiana jest również za pomocą symbolu graficznego – to trójkąt równoramienny, który można również postrzegać jako strzałkę zwróconą w prawo – w miejscu przecięcia się dłuższych ramion znajduje się okrąg styczny do jego wierzchołka (jego średnica to około ¼ długości krótszego boku trójkąta). Wejście na bramkę znajduje się po lewej stronie graficznego przedstawienia (prostopadle do krótkiego ramienia trójkąta), natomiast wyjście jest po prawej od symbolu (za opisanym kołem). Bramka posiada tylko jedno wejście i jedno wyjście. Przykładowy układ scalony (TTL), który zawiera 6 takich bramek (NOT) nosi nazwę “7404”.
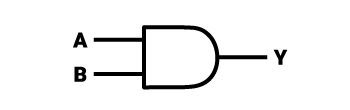
Bramka AND
Przy działaniu bramki logicznej AND wynik 1 można otrzymać tylko w przypadku, kiedy oba wejścia będą równały się jedynce. Tego typu bramki mogą występować w wersjach trzywejściowych, czterowejściowych oraz o znacznie większej liczbie wejść. Należy pamiętać, że niezależnie od tego, ile wejść będzie znajdowało się w stanie wysokim – stan wysoki na wyjściu będzie możliwy tylko w przypadku, jeżeli na każdym wejściu będzie znajdowała się logiczna jedynka.
Przykład 1:
wejście nr 1 = 1
wejście nr 2 = 0
wejście nr 3 = 1
wyjście = 0
Przykład 2:
wejście nr 1 = 1
wejście nr 2 = 1
wejście nr 3 = 1
wyjście = 1
Symbol logiczny bramki AND przypomina figurę zbudowaną z kwadratu oraz połówki koła (przeciętego wzdłuż średnicy, której długość jest równa długości boku kwadratu. Prawy bok kwadratu jest połączony z płaską częścią połowy koła. Całość przypomina strzałkę z wygładzonym grotem, która jest zwrócona w prawą stronę. Po jej lewej stronie, na lewym boku kwadratu umieszczone są wejścia na bramkę, a wyjście analogicznie do symbolu bramki NOT jest po prawej stronie. Przykładowy układ scalony (TTL), który zawiera 4 takie bramki (bramki AND z dwoma wejściami) nosi nazwę “7408”.

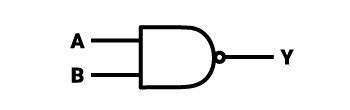
Bramka NAND (-AND)
Dzianie bramki NAND (-AND) jest dokładnie odwrotne do działania bramki AND. Alternatywną nazwą NAND jest określenie “-AND” – myślnik przed oznaczeniem AND oznacza negację. Tak też można interpretować działanie bramki NAND – jest ono dokładnie takie, jakby na wejściu bramki AND zostały umieszczone odpowiednie wartości, na jej wyjściu pojawił się wynik, a następnie został on przepuszczony przez jeszcze bramkę NOT. Można również interpretować działanie NAND w taki sposób, jakby przed każdym z wejść na bramkę AND była bramka NOT. W uproszczeniu działanie bramki NAND można opisać tak – stan niski (0) pojawia się jedynie wtedy, jeżeli na wszystkich wejściach pojawi się stan wysoki (1). Warto zaznaczyć, że bramka NAND posiada nieograniczoną liczbę wejść.
Przykład 1:
wejście nr 1 = 1
wejście nr 2 = 0
wejście nr 3 = 1
wyjście = 1
Przykład 2:
wejście nr 1 = 1
wejście nr 2 = 1
wejście nr 3 = 1
wyjście = 0
Symbol logiczny bramki NAND jest prawie taki sam jak symbol bramki AND. To kwadrat, na którego prawym boku doczepione jest pół okręgu – przecięty wzdłuż średnicy, której wierzchołki stykają się z wierzchołkami kwadratu. Całość przypomina strzałkę z wygładzonym grotem, na końcu którego znajduje się niewielkie koło o średnicy długości około ¼ długości boku kwadratu.Jego średnica jest przedłużeniem promienia półokręgu i znajduje się w połowie wysokości całej figury. Koło jest takie samo, jak to, które zostało opisane przy bramce NOT – oznacza dokładną odwrotność do symbolu, przy którym się znajduje (trójkąt jest symbolem sumy – odwrotnością jest negacja, AND jest negacją NAND). Wejścia do bramki umieszczone są na lewym boku kwadratu, natomiast wyjście znajduje się tuż za małym kołem. Przykładowy układ scalony (TTL), który zawiera 4 takie bramki (bramki NAND z dwoma wejściami) nosi nazwę “7400”, “7401” oraz “7403”.
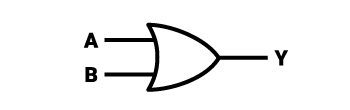
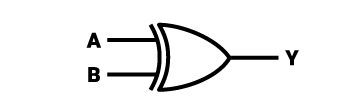
Bramka OR
Na wyjściu bramki OR wynik o wartości 1 pojawi się zawsze w sytuacji, jeżeli chociaż jedno z wejść przyjmuje stan wysoki. Oznacza to również, że jeżeli pojawi się więcej niż jedno wejście o stanie wysokim – na wyjściu również pojawi się jedynka. Tak więc zero pojawi się na wyjściu wyłącznie w sytuacji, kiedy na wszystkich wejściach bramki również ustawione będzie zero. Oczywiście wyjście jest zawsze tylko jedno. Typowy układ zawiera dwa wejścia, ale może posiadać ich nieskończenie wiele i będzie działał na takich samych zasadach.
Przykład 1:
wejście nr 1 = 0
wejście nr 2 = 1
wejście nr 3 = 0
wyjście = 1
Przykład 2:
wejście nr 1 = 1
wejście nr 2 = 1
wejście nr 3 = 1
wyjście = 1
Przykład 3:
wejście nr 1 = 0
wejście nr 2 = 0
wejście nr 3 = 0
wyjście = 0
Symbol logiczny bramki OR kolejny raz przypomina strzałkę. Zdecydowanie można zauważyć podobieństwo do symbolu dla bramki logicznej AND i NAND, ale łatwiej będzie opisać go od nowa. Symbol bramki OR można określić jako figurę, która składa się z połączonego kwadratu i trójkąta równoramiennego, którego długość najkrótszego boku jest równa wysokości boku kwadratu, do którego prawego boku przylega rzeczony trójkąt. Lewy bok kwadratu jest wycięty, a miejsce po wycięciu ma kształt łuku, będącego fragmentem stycznego okręgu o średnicy kilkukrotnie większej niż bok kwadratu. Dwa ramiona przyłączonego trójkąta równoramiennego są wypukłe na zewnątrz, dzięki czemu całość jest bardziej opływowa, przy zachowaniu ostrego zakończenia “strzałki”. Wypukłość można określić, jako stykające się z równymi bokami trójkąta dwa wycinki koła o średnicy kilkukrotnie większej niż dowolny bok trójkąta. Przykładowy układ scalony (TTL), który zawiera 4 takie bramki nosi nazwę “7432”.
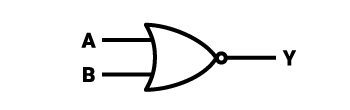
Bramka NOR
Analogicznie do przedstawionych powyżej bramek, można domyślać się jakiego rodzaju działanie przedstawia bramka NOR. Przeglądając poprzednie nazwy, można zauważyć pewną tendencję: bramki, których nazwy zostaną poprzedzone literą N, będą działały dokładnie odwrotnie w stosunku do swojego oryginału. Litera N (od angielskiego not, czyli “nie”) oznacza bowiem negację (jak w przypadku AND i NAND). Działanie bramki NOR można określić jako całkowitą odwrotność działania bramki OR – można spojrzeć na nią, jak na działanie kolejno bramki OR na wszystkie sygnały wejściowe, jakie otrzymała, a następnie wprowadzenie jej sygnału wyjściowego na wejście bramki NOT – wynik będzie wskazywał na działanie bramki NOR. Oczywiście można również założyć, że przed każdym z wejść na bramkę OR zostanie zastosowana bramka NOT – wtedy każde wejście bramki OR będzie pochodziło z wyjścia bramek NOT. Upraszczając opis zasady działania, bramka NOR na wyjściu zawsze zwróci stan niski, z wyjątkiem sytuacji, w której wszystkie stany będą ustawione na wartość 0. Takie bramki mogą mieć nieskończoną ilość wejść.
Przykład 1:
wejście nr 1 = 1
wejście nr 2 = 0
wejście nr 3 = 1
wyjście = 0
Przykład 2:
wejście nr 1 = 0
wejście nr 2 = 0
wejście nr 3 = 0
wyjście = 1
Przykład 3:
wejście nr 1 = 1
wejście nr 2 = 0
wejście nr 3 = 0
wyjście = 0
Symbol graficzny takiej bramki logicznej ponownie jest analogiczny do zmian w wyglądzie, jakie zachodziły między symbolami bramek logicznych, a symbolami bramek logicznych, które były odwrotnością tych pierwszych. Pierwowzór symbolu w wersji z negacją utrzymuje na prawym końcu niewielkie kółko o średnicy przybliżonej długością do ¼ wysokości całej grafiki. W tym wypadku jest to opisywany wcześniej kwadrat, którego lewy bok jest lekko wycięty – kształt wcięcia wygląda jak niewielki wycinek koła o kilkukrotnie większej średnicy niż bok kwadratu. Prawy bok kwadratu przylega do trójkąta równoramiennego, którego boki są zaokrąglone – delikatnie nadbudowane wycinkami koła o bardzo dużej średnicy. Do ostrego zakończenia po prawej przylega niewielkie kółko – graficzny znak oznaczający negację. Z lewej strony znajdują się wejścia do bramki logicznej (na wyciętym boku kwadratu), a za niewielkim kółkiem znajduje się wyjście bramki. Całość wygląda jak jakiś rodzaj pocisku. Przykładowy układ scalony (TTL), który zawiera 4 takie bramki nosi nazwę “7402”.
Bramka XOR (lub inaczej EXOR)
Bramka EXOR (Exclusive-OR, czyli “wyłącznie nie”) to jedna z wyjątkowych funkcji, które nie należą już do grupy najczęściej stosowanych – podstawowych funkcji bramek logicznych. To bramka, która na wejściu ma zawsze dokładnie dwie zmienne (jest to funkcja dwóch zmiennych). Uzyskuje wysoki stan zawsze, jeżeli tylko jeden ze stanów wejściowych jest równy logicznej jedynce. Stan niski na wyjściu pojawi się w sytuacji, jeżeli obie wartości na wejściu będą jednakowe. Bramka XOR wykonuje operacja dodawania bitów modulo-2.
Przykład 1:
wejście nr 1 = 1
wejście nr 2 = 1
wyjście = 0
Przykład 2:
wejście nr 1 = 0
wejście nr 2 = 0
wyjście = 0
Przykład 3:
wejście nr 1 = 1
wejście nr 2 = 0
wyjście = 1
Przykład 4:
wejście nr 1 = 0
wejście nr 2 = 1
wyjście = 1
Reprezentacja graficzna bramki logicznej XOR to symbol, który wygląda podobnie jak reprezentacja graficzna bramki logicznej OR. Bramka XOR w uproszczeniu wygląda jak pocisk, ale dodatkowo posiada linię równolegle ustawioną do lewego boku symbolu. Lewy bok symbolu to była ściana kwadratu, która jest wklęsła w związku z wyciętym fragmentem w kształcie wycinka koła o bardzo dużym promieniu. Opisywana wcześniej równoległa linia umieszczona po lewej stronie od symbolu ma kształt wycinka okręgu o promieniu takim samym jak promień koła, którego wycinek został wycięty z lewego boku kwadratu.
Prawa logiczne
To zdania prawdziwe podczas każdej interpretacji stałych pozalogicznych, które się w nich znajdują. Suma logiczna to zdanie logiczne, zwane również alternatywą, o postaci p lub q.
Bramki logiczne – FAQ
Jak oceniasz ten wpis blogowy?
Kliknij gwiazdkę, aby go ocenić!
Średnia ocena: 4.6 / 5. Liczba głosów: 69
Jak dotąd brak głosów! Bądź pierwszą osobą, która oceni ten wpis.
























5 Responses
pomocne dzięki
Co to sygnal logiczny i stan logiczny
Ponownie ta sama sytuacja dotyczy dodawania względem mnożenia: wrażenie a + b × c jest równe (a+b)×(a+c).
Chyba nie bardzo… 1 + 2 × 3 = 7, (1 + 2) × (1 + 3) = 12
Prawa algebry Boole’a tyczą się zmiennych logicznych, które mogą przyjmować wartość 0 lub 1.
super okok